阪急各線が集結する十三駅近くの全13部屋の大規模スタジオです。その内12部屋は14帖以上の広々としたスタジオ、Lstを除く全部屋は鏡張りのスタジオとなっており、充実した練習環境を備えております。またロビーは明るく広々としつつも、利用者同士が干渉しにくくプライバシーが保たれやすい作りとなっております。
メンテナンスの行き届いた機材設備と親切なスタッフがあなたのご来店をお待ちしております。
2026年3月限定!平日の営業時間を「朝8時から」に拡大します。
Studio246 JUSOの特長

24時間営業
24時間いつでもスタジオ利用が可能、ロッカーへ荷物の出し入れが可能、お電話やご来店による問い合わせ、ご相談が可能です。

専用駐車場
店舗専用駐車場完備。(有料/予約制。駐車可能台数に限りがあります。)

専用自転車/
バイク置き場
店舗専用自転車/バイク置き場完備。(無料。駐車可能台数に限りがあります。)

正面鏡 or 側面鏡
鏡のあるスタジオがあります。
【正面鏡】
ドラムの向かいの壁一面が鏡張り。利用者全員が鏡を見ながら練習することができます。
【側面鏡】
スタジオの壁の半分程度が鏡張り。一部の利用者が鏡を見ながら練習することができます。

一発ライン録音
追加料金なしでスタジオ練習を良音質で録音することが可能です。デモやオーディション用音源にも最適。(店舗でCD-Rを購入して録音する場合はCD-R購入代金が必要です)

各種物販
弦やピックといった楽器用小物はもちろん、飲み物や軽食(一部の店舗に限る)も販売しております。

機材預かりサービス
スタジオをご利用の方は、前後のご都合に合わせて、一時的にスタジオに機材を置いておくことができます。最大で1日程度(前日~スタジオ利用当日、またはスタジオ利用当日~翌日)お預かりいたします。

月極ロッカー/機材庫
スタジオを頻繁に利用される方は、鍵付きのロッカー/機材庫をご使用いただくことができます。(※スタジオ利用頻度/機材量等の使用要件があります。)

インターネット環境
スタジオロビー、および部屋内にインターネット環境があります。
無線(Wi-fi)での接続ができる場合と、有線(LANケーブル)での接続ができる場合があります。(※店舗をご利用の方みなさまが使用するインターネット環境ですので、確実に安定した接続環境をお約束できるものではありません。)

完全分煙
非喫煙者の方が安心してご利用いただけるよう、喫煙スペースが完全に分かれています。

スタジオLIVE
スタジオライブが可能な部屋があります。詳しくはこちら。

セルフREC
セルフレコーディング専用ルーム/設備があります。詳しくはこちら。
Price 料金表
スタジオ246ではあらゆる方に安心・満足してご利用いただけるよう、「曜日」「時間帯」「人数」「スタジオ」によって異なる料金区分を設けております。
「4人で予約したけど、1人来ることができなかった」といった場合でもお申し出いただければ、「スタジオに入られた人数」で料金を計算いたしますので安心してご予約ください。
通常練習料金
5st・Lst 以外
| ご利用人数 | 曜日 | 朝~夕 (最大OPEN~ 19:30) |
夕~深夜 (最大19:00 ~ 23:30) |
深夜~朝 (最大23:00 ~ CLOSE) |
|---|---|---|---|---|
| 2名様以下 | 平日 | 1,840円 /1h | 2,200円 /1h | 1,840円 /1h |
| 土日祝 | 2,260円 /1h | |||
| 3名様 | 平日 | 2,220円 /1h | 2,790円 /1h | 2,220円 /1h |
| 土日祝 | 2,910円 /1h | |||
| 4~5名様 | 平日 | 2,380円 /1h | 2,920円 /1h | 2,380円 /1h |
| 土日祝 | 3,120円 /1h | |||
| 6名様以上 | 平日 | 2,760円 /1h | 3,240円 /1h | 2,760円 /1h |
| 土日祝 | 3,420円 /1h | |||
5st 料金
| ご利用人数 | 曜日 | 朝~夕 (最大OPEN~ 19:00) |
夕~深夜 (最大19:00 ~ 23:30) |
深夜~朝 (最大23:00 ~ CLOSE) |
|---|---|---|---|---|
| 2名様以下 | 平日 | 1,600円 /1h | 1,800円 /1h | 1,600円 /1h |
| 土日祝 | 2,000円 /1h | |||
| 3名様 | 平日 | 1,980円 /1h | 2,460円 /1h | 1,980円 /1h |
| 土日祝 | 2,580円 /1h | |||
| 4名様以上 | 平日 | 2,160円 /1h | 2,640円 /1h | 2,160円 /1h |
| 土日祝 | 2,880円 /1h | |||
Lst 料金
| 利用人数 | 曜日 | 朝~夕 (最大OPEN~ 19:00) |
夕~深夜 (最大19:00 ~ 23:30) |
深夜~朝 (最大23:00 ~ CLOSE) |
|---|---|---|---|---|
| 何名様でも | 平日 | 2,760円 /1h | 3,240円 /1h | 2,760円 /1h |
| 土日祝 | 3,420円 /1h | |||
※スタジオライブご利用時の料金は⇒コチラ
時間帯の切り替わり時間
- 00分スタートのご予約
-
- 朝~夕OPEN~19:00
- 夕~深夜19:00~23:00
- 深夜~朝23:00~CLOSE
- 30分スタートのご予約
-
- 朝~夕OPEN~19:30
- 夕~深夜19:30~23:30
- 深夜~朝23:30~CLOSE
ロングタイム割引練習料金
平日昼間と毎日深夜は、めちゃめちゃお得なロングタイム割引料金が適用可能なので3時間以上の利用がオススメ!
適用時間内であれば、何時間の利用でもOK!上手に使って効率的にスタジオ練習しましょう!
- 割引適用時間帯
-
- 平日朝~夕(最大 OPEN〜19:30)
- 毎日深夜~朝(最大 23:00〜CLOSE)
5st 以外
| ご利用人数 | 3時間 | 4時間 | 5時間 | 6時間 | 7時間 |
|---|---|---|---|---|---|
| 2名様以下 | 通常5,520円4,800円 | 通常7,360円6,000円 | 通常9,200円7,200円 | 通常11,040円8,400円 | 1,200円追加 / 1h |
| 3名様 | 通常6,660円5,520円 | 通常8,880円6,720円 | 通常11,100円7,920円 | 通常13,320円9,120円 | 1,200円追加 / 1h |
| 4~5名様 | 通常7,140円6,040円 | 通常9,520円7,320円 | 通常11,900円8,600円 | 通常14,280円9,880円 | 1,280円追加 / 1h |
| 6名様以上またはLst | 通常8,280円6,780円 | 通常11,040円8,240円 | 通常13,800円9,700円 | 通常16,560円11,160円 | 1,460円追加 / 1h |
5st
| ご利用人数 | 3時間 | 4時間 | 5時間 | 6時間 | 7時間 |
|---|---|---|---|---|---|
| 2名様以下 | 通常4,800円4,180円 | 通常6,400円5,140円 | 通常8,000円6,100円 | 通常9,600円7,060円 | 960円追加 / 1h |
| 3名様 | 通常5,940円4,860円 | 通常7,920円5,880円 | 通常9,900円6,900円 | 通常11,880円7,920円 | 1,020円追加 / 1h |
| 4名様以上 | 通常6,480円5,130円 | 通常8,640円6,200円 | 通常10,800円7,270円 | 通常12,960円8,340円 | 1,070円追加 / 1h |
個人練習料金
- 1名様
- 620円 /1h
個人練習の受付時間は、前日の朝7:00からです。
個人練習料金は、3名以下の利用に適用することができます。
上記要件を満たすご予約は、自動的に個人練習料金でご利用いただけます。
キャンセル料金表
| 2日前 | 前日 | 当日 |
|---|---|---|
| スタジオ料金の60% | スタジオ料金の80% | スタジオ料金の100% |
キャンセル料金の計算のため、日付の切り替わり時間は、朝7:00とさせていただきます。
キャンセル料金は、ご予約された同じ日の予約時間の移動・変更でも発生しますので予めご了承ください。
予約日時の変更(同日内の時間変更を含む)、予約時間の短縮はキャンセル扱いとなり料金が発生します。
Studio スタジオ紹介
1 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

2 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

3 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

4 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

5 Studio
9畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom

6 Studio
15畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

7 Studio
15畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

8 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

9 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

10 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

11 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

12 Studio
14畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

L studio
36畳
常設機材
- ギターアンプ
-
- Marshall DSL100H
- Roland JC-120
- ベースアンプ
-
- Hartke HA3500
- ドラムセット
-
- Pearl MastersCustom
- キーボード
-
- 電子ピアノ / YAMAHA CP-40

Studio Map
Studio246 JUSO
スタジオマップ

お気に入りのあの機材がレンタルできる!
機材レンタルサービス
Access アクセス
osaka / 大阪 十三
Studio246 JUSO
- 住所
- 〒532-0024
大阪府大阪市淀川区十三本町1丁目7-27 サンポードシティビル4F
- 最寄駅
- 全線「十三」駅西改札口から徒歩2分
- 営業時間
-
月曜日〜金曜日 9:00〜翌朝5:00 土曜日・日曜日 8:00〜翌朝5:00
2026年3月限定!毎朝8時OPEN!
 専用駐輪場について
専用駐輪場について
駐輪料金は無料です。
初めてご利用される場合は、246JUSO受付にて駐輪場の契約(無料)を行ってください。
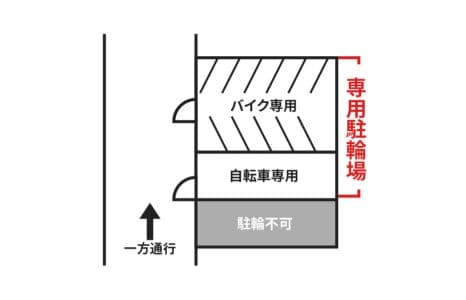
- 下図、駐輪場内の「専用駐輪場」エリアにお停めいただけます。
- 敷地内は「バイク専用駐輪場」「自転車専用駐輪場」に分かれています。所定の場所以外の駐輪はご遠慮ください。
- 駐輪可能台数は限られております。予約制ではありませんので、満車の場合は停められない場合もございます。
当店ご利用時以外にお停めされている場合や、悪質な利用と当方が判断した場合、撤去移動又は通報をする場合もございます。予めご了承ください。
-
場所

-
駐輪場内